Berita Terbaru: Aerosol

An aerosol is a suspension of fine solid particles or liquid droplets in a gas.Examples are clouds, and air pollution such as smog and smoke. In general conversation, aerosol usually refers to an aerosol spray can or the output of such a can. Aerosols have many technological applications including aerosol sprays; dispersal of pesticides; medical treatment of respiratory illnesses and in combustion technology.Aerosol science covers a wide range of topics, such as generation and removal of aerosols, technological application and their impacts on the environment and people.

Definitions

Photomicrograph made with a Scanning Electron Microscope (SEM): Fly ash particles at 2,000x magnification. Most of particles in this aerosol are nearly spherical.

An aerosol is defined as a suspension of solid or liquid particles in a gas. This includes both the particles and the suspending gas, which is usually air.^[1] The name aerosol is thought to have been first used by F.G. Donnan during World War I to describe clouds of microscopic particles in air. This term was an analogy to a liquid colloid suspension called a hydrosol.^[3] A primary aerosol has particles that are introduced directly into the gas and secondary aerosols are formed when gas-to-particle conversion occurs.^[4]
There are several measures of aerosol concentration. The most important in the area of environmental science and health is the mass concentration (M), defined as the mass of particulate matter per unit volume with units such as μg/m³. Also commonly used is the number concentration (N), the number of particles per unit volume with units such as number/m³ or number/cm³.^[5]
The size of particles has a major influence on their properties and the aerosol particle radius or diameter (d_p) is a key property used to characterise aerosols. If all the particles in an aerosol are the same size it is known as monodisperse and this type of aerosol can be produced in the laboratory. Most aerosols however are polydisperse, i.e. they have a range of particle sizes.^[6] While liquid droplets are nearly always spherical, solid particles have a variety of shapes and to understand their properties, a equivalent diameter is used. The equivalent diameter is the diameter of a regular particle which has the same value of some physical property as the irregular particle.^[7] The equivalent volume diameter (d_e) is defined as the diameter of a sphere having the same volume as that of the irregular particle.^[8] Also commonly used is the aerodynamic diameter.

[edit] Size distribution

The same hypothetical log-normal aerosol distribution plotted, from top to bottom, as a number vs diameter distribution, a surface area vs diameter distribution, and a volume vs diameter distribution. Typical mode names are shows at the top. Each distribution is normalise so that the total area is 1000.

For a monodisperse aerosol, a single number - the particle diameter - suffices to describe the size of the particles. However, for a polydisperse aerosol, we describe the size of the aerosol by use of the particle-size distribution. This defines the relative amounts of particles present, sorted according to size. One approach to defining the particle size distribution is to use a list of the size of all particles in a sample. However, this approach is awkward to use so other solutions have been found. Another approach is to split the complete size range into intervals and find the number of particles in each interval. This data can then be visualised using a histogram where the area of each bar represents the total number of particles in that size bin, usually normalised by dividing the number of particles in an interval by the width of the interval and by the total number of particles so that the total area is equal to 1 and the area of each bar is equal to the proportion of all particles in that size range. If the width of the bins tends to zero we get the frequency function:

$df = f(d_p) \,\mathrm{d}d_p$

where

$d_p$ is the diameter of the particles

$\,\mathrm{d}f$ is the fraction of particles having diameters between $d_p$ and $d_p$ + $\mathrm{d}d_p$

$f(d_p)$ is the frequency function

Therefore the area under the frequency curve between two sizes a and b represents the total fraction of the particles in that size range:

$f_{ab}=\int_a^b f(d_p) \,\mathrm{d}d_p$

It can also be formulated in terms of the total number density N:

$dN = N(d_p) \,\mathrm{d}d_p$

If we assume the aerosol particles are spherical, we then find that the aerosol surface area per unit volume (S) is given by the second moment:

$S= \pi/2 \int_0^\infty N(d_p)d_p^2 \,\mathrm{d}d_p$

and the third moment gives the total volume concentration (V) of the particles:

$V= \pi/6 \int_0^\infty N(d_p)d_p^3 \,\mathrm{d}d_p$

It can also be useful to approximate the particle size distribution using a mathematical function. The normal distribution is not usually suitable as most aerosols have a skewed distribution with a long tail of larger particles. Also for a quantity that varies over a large range, as many aerosol sizes do, the width of the distribution implies negative particles sizes which is clearly not physically realistic. However, the normal distribution can be suitable for some aerosols, such as test aerosols, certain pollen grains and spores.
A more widely chosen distribution is the log-normal distribution where the number frequency is given as:

$df = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(d_p - \bar{d_p})^2}{2 \sigma^2} }\mathrm{d}d_p$

where:

$\sigma$ is the standard deviation of the size distribution and

$\bar{d_p}$ is the arithmetic mean diameter.

The log-normal distribution has no negative values, can cover a wide range of values and fits observed size distributions reasonably well.
Other distributions which can be used to characterise particle size are: the Rosin-Rammler distribution, applied to coarsely dispersed dusts and sprays; the Nukiyama-Tanasawa distribution, for sprays having extremely broad size ranges; the power function distribution, which has been applied to atmospheric aerosols; the exponential distribution, applied to powdered materials and for cloud droplets the Khrgian-Mazin distribution.

[edit] Physics

[edit] Terminal velocity of a particle in a fluid

For low values of the Reynolds number (<1), which is true of most aerosol motion, Stokes' law describes the force of resistance on a solid spherical particle in a fluid. However, Stoke's law is only valid when the velocity of the gas at the particle's surface is zero. For small particles (< 1 μm) this assumption breaks down. This can be accounted for by introducing the Cunningham correction factor which is always greater than 1. Including this factor we find that the relation between the resisting force on a particle and its velocity is: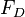

$F_D = \frac {3 \pi \eta V d}{C_c}$

where

$F_D$ is the resisting force on a spherical particle

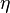$\eta$ is the viscosity of the gas

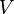$V$ is the particle velocity

$C_c$ is the Cunningham correction factor.

This allows us to calculate the terminal velocity of a particle undergoing gravitational settling in still air. Neglecting buoyancy effects we find:

$V_{TS} = \frac{\rho_p d^2 g C_c}{18 \eta}$

where

$V_{TS}$ is the terminal settling velocity of the particle.

The terminal velocity can also be derived for other kinds of forces. If Stoke's law holds then the resistance to motion is directly proportional to speed. The constant of proportionality is the mechanical mobility (B) of a particle:
$B = \frac{V}{F_D} = \frac {C_c}{3 \pi \eta d}$
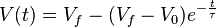
If a particle is travelling a velocity other than its terminal velocity it approaches the terminal velocity exponentially with an e-folding time equal to the relaxation time: $V(t) = V_{f}-(V_{f}-V_{0})e^{-\frac{t}{\tau}}$
where:

$V(t)$ is the particle speed at time t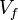

$V_f$ is the final particle speed

$V_0$ is the initial particle speed

To account for the effect of the shape non-spherical particles, a correction factor known as the dynamic shape factor is applied to Stoke's law. It is defined as the ratio of the resistive force of the irregular particle to that of a spherical particle with the same volume and velocity:
$\chi = \frac{F_D}{3 \pi \eta V d_e}$
where:

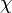$\chi$ is the dynamic shape factor

[edit] Aerodynamic diameter

The aerodynamic diameter of an irregularly shaped particle is defined as the diameter of the spherical particle with a density of 1000 kg/m³ that has the same settling velocity as the irregular particle.^[22]
Neglecting the slip correction, the terminal velocity at which the particle settles is proportional to the square of the aerodynamic diameter, d_a:^[22]

$V_{TS} = \frac{\rho_0 d_a^2 g}{18 \eta}$

where

$\ \rho_0$ = standard particle density (1000 kg/m³).

The aerodynamic diameter can be shown to be given by:^[23]

$d_a=d_e\left(\frac{\rho_p}{\rho_0 \chi}\right)^{\frac{1}{2}}$

The aerodynamic diameter is commonly applied to particulate pollutants and inhaled drugs to predict where in the respiratory tract such particles will deposit. Drug particles for pulmonary delivery are typically characterized by aerodynamic diameter rather than geometric diameter.^{[citation needed]}

[edit] Dynamics

The previous discussion focussed on single aerosol particles. In contrast, aerosol dynamics explains the evolution of complete aerosol populations. The concentrations of particles will change over time as a result of many processes. External processes which move particles across the wall of a volume of gas include diffusion, gravitational settling and migration caused by external forces such as electric charges. A second set of processes are internal to a given volume of gas are particle formation (nucleation), evaporation or chemical reaction and coagulation.^[24]
The evolution of the aerosol due to these process can be characterized by a differential equation called the Aerosol General Dynamic Equation (GDE).^[24]
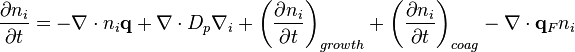
$\frac{\partial{n_i}}{\partial{t}} = -\nabla \cdot n_i \mathbf{q} +\nabla \cdot D_p\nabla_i + \left(\frac{\partial{n_i}}{\partial{t}}\right)_{growth} + \left(\frac{\partial{n_i}}{\partial{t}}\right)_{coag} -\nabla \cdot \mathbf{q}_F n_i$
Change in time = Convective transport + brownian diffusion + gas-particle interactions + coagulation + migration by external forces
Where:

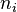$n_i$ is number density of particles of size category $i$

$\mathbf{q}$ is the particle velocity

$D_p$ is the particle Stokes-Einstein diffusivity

$\mathbf{q}_F$ is the particle velocity associated with an external force

[edit] Coagulation

When particles are present in an aerosol they collide with each other. During that they may undergo coalescence or aggregation. This process leads to a change in the aerosol number/size distribution function, with the mode growing in diameter and decreasing in number.

[edit] Dynamics regimes

There are three different dynamical regimes which govern the behaviour of an aerosol, which can be defined by the Knudsen number of the particle

$K_n=\frac{2\lambda}{d}$

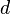where $\lambda$ is the mean free path of the suspending gas and $d$ is the diameter of the particle. Particles are in the free molecular regime when K_n >> 1, that is particles are small compared to the mean free path of the suspending gas. In this regime, particles interact with the suspending gas through a series of 'ballistic' collisions with gas molecules. As such, they behave similarly to gas molecules, tending to follow streamlines and diffusing rapidly through Brownian motion. The mass flux equation in the free molecular regime is:

$I = \frac{\pi a^2}{k_b} \left( \frac{P_\infty}{T_\infty} - \frac{P_A}{T_A} \right) \cdot C_A \alpha$

where a is the particle radius, P_∞ and P_A are the pressures far from the droplet and at the surface of the droplet respectively, k_b is the Boltzmann constant, T is the temperature, C_A is mean thermal velocity and α is mass accommodation coefficient^{[citation needed]}. It is assumed in the derivation of this equation that the pressure and the diffusion coefficient are constant.
Particles are in the continuum regime when K_n << 1. In this regime, the particles are big compared to the mean free path of the suspending gas, meaning that the suspending gas can be though of as a continuous fluid flowing round the particle. The molecular flux in this regime is:

$I_{cont} \sim \frac{4 \pi a M_A D_{AB}}{RT} \left( P_{A \infty} - P_{AS}\right)$

where a is the radius of the particle A, M_A is the molecular mass of the particle A, D_AB is the diffusion coefficient between particles A and B, R is the ideal gas constant, T is the temperature in kelvins and P are the pressures at infinite and at the surface respectively^{[citation needed]}.
The transition regime contains all the particles in between the free molecular and continuum regimes or K_n ≈ 1. The forces experienced by a particle are a complex combination of interactions with individual gas molecules, and macroscopic interactions. The semi-empirical equation describing mass flux is:

$I = I_{cont} \cdot \frac{1 + K_n}{1 + 1.71 K_n + 1.33 {K_n}^2}$

where I_cont is the mass flux in the continuum regime^{[citation needed]}. This formula is called the Fuchs-Sutugin interpolation formula. These equations don’t take into account the heat release effect.

[edit] Partitioning

Condensation and evaporation

Aerosol partitioning theory governs the condensation and evaporation of substances to and from an aerosol surface, respectively. Condensation of mass causes the mode of an aerosol number/size distribution to grow to larger diameters. Conversely, evaporation moves the mode to smaller diameters. Nucleation is the process of forming aerosol mass from the condensation of a gaseous precursor, specifically a vapour. In order for the vapour to condense, it must be supersaturated i.e. its partial pressure must be greater than its vapour pressure. This can happen for three reasons^{[citation needed]}:

If the vapour pressure is lowered by lowering the temperature of the vapour
If chemical reactions increase the partial pressure of a gas, or lower its vapour pressure
If the addition of another vapour lowers the equilibrium vapour pressure due to the Raoult Effect

There are two types of nucleation processes. Gases will preferentially condense onto pre-existing surfaces (e.g. aerosol particles), which is known as heterogeneous nucleation. This causes the number/size distribution mode diameter to increase with the total number concentration remaining constant. If the supersaturation is high enough, and no suitable surfaces are present, particles may condense in the absence of a pre-existing surface, which is known as homogeneous nucleation. The emergence of a number/size distribution mode growing from a diameter of zero.

[edit] Activation

Aerosols are said to be activated when they become coated by water, usually in the context of forming a cloud droplet^{[citation needed]}. Following the Kelvin effect (based on the curvature of liquid droplets) smaller particles need a higher ambient relative humidity to maintain equilibrium than bigger ones would. Relative humidity (%) for equilibrium can be determined from the following formula:

$RH = \frac{p_s}{p_0} \times 100% = S \times 100%$

where $p_s$ is the saturation vapor pressure above a particle at equilibrium (around a curved liquid droplet), p₀ is the saturation vapor pressure (flat surface of the same liquid) and S is the saturation ratio.
Kelvin equation for saturation vapor pressure above a curved surface is:

$\ln{p_s \over p_0} = \frac{2 \sigma M}{RT \rho \cdot r_p}$

where r_p droplet radius, σ surface tension of droplet, ρ density of liquid, M molar mass, T temperature, and R molar gas constant.

[edit] Solution to the General Dynamic Equation

There are no general solutions to the General Dynamic Equation (GDE) - common methods used to solve the GDE are:^{[citation needed]}

Moment method
Modal/Sectional Method
Quadrature Method of Moments.

Berita Terbaru

Selasa, 15 Januari 2013

Aerosol

Definitions

[edit] Size distribution

[edit] Physics

[edit] Terminal velocity of a particle in a fluid

[edit] Aerodynamic diameter

[edit] Dynamics

[edit] Coagulation

[edit] Dynamics regimes

[edit] Partitioning

[edit] Activation

[edit] Solution to the General Dynamic Equation

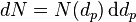
Tidak ada komentar:

Posting Komentar

Mengenai Saya

Arsip Blog